Chapter 6 Geotech Engineering Laboratory: Soil Permeability

Chapter 6 Geotech Engineering Laboratory: Soil Permeability#

  1. Introduction: Soil Density Lab

  2. Simulation: Procter density Test

  3. Self-Assessment

1. Introduciton#

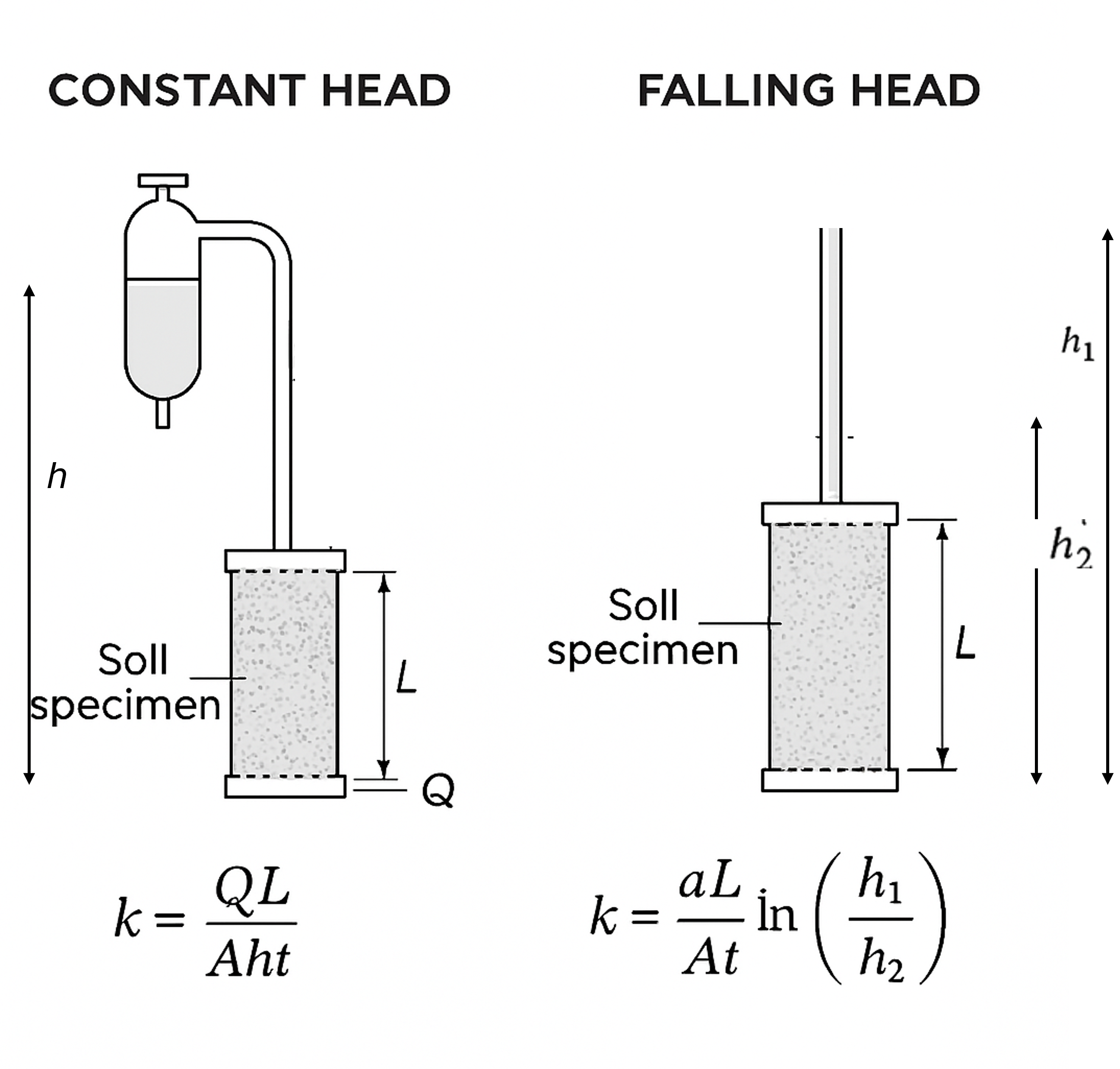
Descriptive alt text for accessibility

Fig. 18 **Figure 4.4 **: Constant and Falling head method for the measurement of Soil permeability#

🌱 Soil Permeability – Definition, Importance & Applications in Geotechnical Engineering#

Soil permeability is the ability of soil to allow fluids (typically water) to pass through its pores. It is quantified as hydraulic conductivity (K), usually expressed in meters per second (m/s). Permeability depends on particle size, gradation, pore continuity, compaction, and water viscosity.

🔍 Importance for Geotechnical Parameters#

Parameter

Role of Permeability

Hydraulic Conductivity (K)

Core index for water flow through soil

Seepage Analysis

Predicts water migration in slopes, dams, foundations

Settlement Prediction

Influences consolidation rates in saturated clays

Piping & Erosion

High permeability can trigger internal erosion

Bearing Capacity

Excess pore pressure dissipation depends on K

Compaction Control

Impacts drying behavior and strength development

🏗️ Applications in Geotechnical Engineering#

Application

How Permeability Is Used

Earth Dams & Embankments

Controls seepage paths and filter design

Retaining Structures

Affects hydrostatic pressure and drainage planning

Slope Stability

Low K may cause perched water, triggering failure

Foundation Design

Guides dewatering and settlement estimation

Soil Stabilization

Determines chemical injection feasibility

Landfills & Liners

Impermeable layers designed for containment

🧪 Measurement Methods#

Lab Test

Description

Constant Head Test

Measures flow under steady-state conditions (sandy soils)

Falling Head Test

Suitable for low-permeability soils (silts, clays)

Field Permeability

Includes borehole tests, double-ring infiltrometers

🧪 Permeability Testing in Soil Mechanics#

Permeability quantifies how easily water flows through soil pores. It’s typically expressed as hydraulic conductivity (K) in m/s. The choice of test method depends on the expected flow rate and soil type.

📉 Falling Head Method (Best for Clay and Silts)#

🔍 Why Use for Fine-Grained Soils:#

  • Low permeability makes steady-state flow impractical

  • Transient flow enables sensitive head decay measurement

🛠️ Test Principle:#

  • A standpipe is filled to initial head \(( h_1 \))

  • Water infiltrates through specimen over time \(( t \))

  • Final head \(( h_2 \)) is recorded

  • Compute K using:

    \[ K = \frac{aL}{At} \ln\left(\frac{h_1}{h_2}\right) \]

📎 Parameters:#

Symbol

Meaning

\(( a \))

Cross-section of standpipe

\(( A \))

Cross-section of soil specimen

\(( L \))

Length of specimen

\(( h_1, h_2 \))

Initial and final head levels

\(( t \))

Time elapsed during fall

💧 Constant Head Method (Best for Sandy Soils)#

🔍 Why Use for Coarse-Grained Soils:#

  • High flow rates permit steady measurement

  • Flow stabilizes quickly under constant head

🛠️ Test Principle:#

  • Constant head ( h ) is applied to specimen

  • Measure volume ( V ) collected over time ( t )

  • Compute flow rate ( q = V/t )

  • Compute K using:

    \[ K = \frac{qL}{Ah} \]

📎 Parameters:#

Symbol

Meaning

\(( q \))

Discharge rate

\(( A \))

Cross-section of soil specimen

\(( L \))

Length of specimen

\(( h \))

Head difference across specimen

🌡️ Temperature Correction – Influence of Viscosity#

Water viscosity affects how easily it moves through pores. Since viscosity decreases with temperature:

🔍 Correction Formula:#

To adjust measured conductivity to standard temperature (usually 20°C):

\[ K_{20} = K_T \times \frac{\mu_T}{\mu_{20}} \]

Symbol

Meaning

\(( K_T \))

Measured conductivity at test temp

\(( K_{20} \))

Corrected conductivity at 20°C

\(( \mu_T \))

Dynamic viscosity at test temp

\(( \mu_{20} \))

Viscosity at standard temp (≈ 1.002 × 10⁻³ Pa·s)

🌡️ Temperature Effects:#

Temp (°C)

Viscosity ( \mu ) (Pa·s)

Effect on K

10°C

~1.308 × 10⁻³

Lower K (more resistance)

20°C

~1.002 × 10⁻³

Standard reference

30°C

~0.797 × 10⁻³

Higher K (less resistance)

✅ Summary#

Test Method

Suitable Soils

Typical K Range

Falling Head

Clays, Silts

< ( 10^{-7} ) m/s

Constant Head

Sands, Gravels

( 10^{-4} )–( 10^{-2} ) m/s

📊 Empirical Equations for Estimating Soil Permeability#

📘 Based on Particle Size Distribution#

Equation

Expression

Parameters

Soil Type

Kozeny–Carman (simplified)

\(( K = C \cdot \frac{D_{10}^2}{e^2} \cdot \frac{1}{1+e} \))

\(( D_{10} \)): effective grain size

Sand, silt

\(( e \)): void ratio

Hazen’s Equation

\(( K = C \cdot D_{10}^2 \))

\(( D_{10} \)): grain size (cm)

Clean sands

\(( C \)): empirical (~1–1.5)

Chapuis Modification

\(( K = C \cdot D_{10}^2 \cdot \left( \frac{n^3}{1-n^2} \right) \))

\(( n \)): porosity

Sandy to silty soils

🧪 Based on Atterberg Limits#

Equation (Empirical)

Expression

Parameters

Soil Type

Seed et al. (1961)

\(( K = 10^{-7 + 3.3 \cdot PI/LL} \))

PI: Plasticity Index

Fine-grained soils (clays)

Ferguson & Maxwell (1990)

\(( \log(K) = A - B \cdot LL \))

LL: Liquid Limit

Clayey soils

A, B: empirical constants

Morin & Todorovic (1979)

\(( K = a \cdot e^b \cdot LL^{-c} \))

e: void ratio

Silty clays, loams

🧭 Notes#

  • Most empirical formulas provide approximate hydraulic conductivity (K) in m/s or cm/s

  • Empirical constants vary by region, soil genesis, and calibration dataset

  • These formulas are best used for screening, not as substitutes for lab tests

References#

[Das, 2010] Includes detailed procedures for permeability testing. [ASTM International, 2022] Describes the constant head method for measuring hydraulic conductivity in coarse-grained soils like sands and gravels. It uses rigid or flexible wall permeameters under saturated conditions and low hydraulic gradients. [ASTM International, 2016] Provides multiple methods—including falling head and constant head—for testing fine-grained soils using a flexible wall permeameter. It allows for control of effective stress and is suitable for low-permeability materials.

2. Simulation#

🧪 Summary: Permeability Test Calculator (Interactive)#

An interactive Python tool built with ipywidgets to compute hydraulic conductivity (K) of soil using either the Constant Head or Falling Head permeability test methods. It mimics ASTM lab procedures for evaluating water flow through soil specimens.

Test Selection#

  • Users toggle between Constant Head (steady flow) or Falling Head (declining flow)

Input Parameters#

Input Field

Description

Area (m²)

Cross-sectional area of soil specimen

Length (m)

Length of soil column or mold

Volume, Time, Head (Const.)

Flow volume, duration, and head applied

h₁, h₂, t, a (Falling Head)

Initial & final head, elapsed time, pipe area

Computations#

  • Constant Head:
    \(( K = \frac{qL}{Ah} \)), with \(( q = V/t \))

  • Falling Head:
    \(( K = \frac{aL}{At} \ln\left(\frac{h_1}{h_2}\right) \))

Interpretation#

Outputs:

  • Hydraulic Conductivity (K) in m/s

  • Estimated flow regime (clay, silt, sand, gravel) based on K value

📊 How to Interpret Results#

Output Field

Meaning

K Value

Rate at which water flows through soil under gravity

Flow Regime Estimate

Qualitative inference: e.g., clay (low), sand (high)

Error Messages

Triggered for invalid head inputs or negative conductivity

🔍 Typical Hydraulic Conductivity Ranges#

Soil Type

K Value (m/s)

Tight Clay

< 1 × 10⁻⁷

Silty or Loamy Soil

1 × 10⁻⁷ to 1 × 10⁻⁵

Sand/Gravel

> 1 × 10⁻³

✅ Use this tool for classroom demonstrations, lab simulation, or quick validation of flow behavior in compacted or natural soils.

import ipywidgets as widgets
from IPython.display import display, Markdown
import numpy as np

# 🎛️ Style
style = {'description_width': '220px'}
layout = widgets.Layout(width='420px')

# 🧭 Test selection
test_type = widgets.ToggleButtons(
    options=['Constant Head', 'Falling Head'],
    description='Select Test Type:',
    style=style
)

# 📋 Common inputs
area_input = widgets.FloatText(value=0.00075, description='Cross-sectional Area (m²):', style=style, layout=layout)
length_input = widgets.FloatText(value=0.15, description='Length of Specimen (m):', style=style, layout=layout)

# 💧 Constant Head Inputs
volume_input = widgets.FloatText(value=0.003, description='Collected Volume (m³):', style=style, layout=layout)
time_input = widgets.FloatText(value=120, description='Collection Time (s):', style=style, layout=layout)
head_input = widgets.FloatText(value=0.25, description='Head Difference h (m):', style=style, layout=layout)

# 📉 Falling Head Inputs
initial_head = widgets.FloatText(value=0.30, description='Initial Head h₁ (m):', style=style, layout=layout)
final_head = widgets.FloatText(value=0.10, description='Final Head h₂ (m):', style=style, layout=layout)
fall_time = widgets.FloatText(value=240, description='Elapsed Time (s):', style=style, layout=layout)
standpipe_area = widgets.FloatText(value=0.0002, description='Standpipe Area (m²):', style=style, layout=layout)

run_btn = widgets.Button(description='Compute Permeability', layout=widgets.Layout(width='220px'))

# 🔎 Permeability functions
def compute_constant_head(A, L, V, t, h):
    q = V / t
    K = (q * L) / (A * h)
    return round(K, 6)

def compute_falling_head(A, a, L, h1, h2, t):
    if h1 <= h2 or h1 <= 0 or h2 <= 0:
        return None
    ln_ratio = np.log(h1 / h2)
    K = (a * L / (A * t)) * ln_ratio
    return round(K, 6)

# 📄 Output handler
def on_click(b):
    A = area_input.value
    L = length_input.value

    if test_type.value == 'Constant Head':
        V = volume_input.value
        t = time_input.value
        h = head_input.value
        K = compute_constant_head(A, L, V, t, h)
        method = "Constant Head"
    else:
        a = standpipe_area.value
        h1 = initial_head.value
        h2 = final_head.value
        t = fall_time.value
        K = compute_falling_head(A, a, L, h1, h2, t)
        method = "Falling Head"

    if K is None or K <= 0:
        display(Markdown(f"### ❌ Invalid inputs or calculation error. Please verify head levels and time."))
        return

    regime = (
        "🪨 Tight clay or compact silt" if K < 1e-7 else
        "🌾 Silty or loamy soil" if K < 1e-5 else
        "🌊 Coarse sand or gravel"
    )

    md = f"""
### 🧪 Permeability Test Result

- **Method**: {method}  
- **Hydraulic Conductivity (K)**: {K:.6f} m/s  
- **Flow Regime Estimate**: {regime}

---

### 📐 Interpretation
- Typical **K < 1e-7 m/s** → Low permeability (fine soils)  
- Typical **K ~ 1e-5 to 1e-3 m/s** → Medium to high permeability  
- Values > 1e-2 m/s → Highly permeable media (gravel, fractured rock)
"""
    display(Markdown(md))

run_btn.on_click(on_click)

# 🧩 Dynamic Layout
def update_ui():
    if test_type.value == 'Constant Head':
        inputs = [area_input, length_input, volume_input, time_input, head_input]
    else:
        inputs = [area_input, length_input, standpipe_area, initial_head, final_head, fall_time]
    display(widgets.VBox([test_type] + inputs + [run_btn]))

test_type.observe(lambda change: update_ui(), names='value')
update_ui()

3. Self-Assessment#

🔍 Conceptual Questions#

  1. What are the physical principles that distinguish the constant head and falling head methods?

  2. Why is the falling head test more appropriate for fine-grained soils like clays?

  3. How does hydraulic conductivity relate to soil structure and pore connectivity?

  4. What role does specimen geometry (area, length) play in permeability calculations?

  5. Why is flow assumed laminar in these tests—and what happens if it’s not?

💭 Reflective Questions#

  1. Have you observed a soil type where constant head measurements became unstable? What caused it?

  2. If your falling head test shows minimal change in head over time, how do you interpret that about permeability?

  3. What lab challenges might affect the accuracy of time measurements or head readings?

  4. How would you explain the significance of temperature correction to a field technician unfamiliar with fluid viscosity?

  5. Which test method gives you greater confidence for quality assurance in low-permeability soils, and why?

Test Matching#

Q1. Which test is ideal for measuring permeability of saturated clay specimens?
A. Constant Head
B. Falling Head ✅
C. Cone Penetration
D. Plate Load

Q2. Constant head tests typically require which soil condition?
A. Frozen
B. Loose gravel ✅
C. High plasticity
D. Organic-rich silt

Calculation Logic#

Q3. The falling head conductivity formula includes which mathematical function?
A. Square root
B. Logarithm ✅
C. Sine
D. Linear slope

Q4. In constant head tests, discharge rate (q) is calculated as:
A. Time divided by head
B. Length times head
C. Volume divided by time ✅
D. Area times velocity

Interpretation#

Q5. A K value of 1 × 10⁻⁶ m/s most likely corresponds to:
A. Highly permeable gravel
B. Silty or loamy soil ✅
C. Compacted clay
D. Saturated sand dune

Contents