Chapter 3 Hydraulics:Channel Design

1. Introduction: Channel Design

2. Simulation: Channel Design

3. Simulation: Design method selector

4. Self-Assessment

1. Introduction

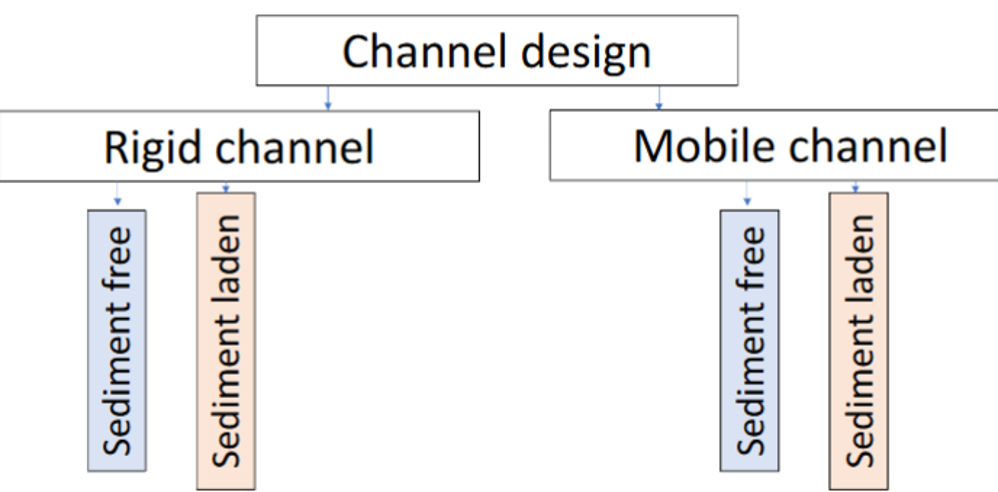
Fig. 11 **Figure 3.11 **: Channel Types

🌊 Canals and Channels: Types, Design Methods, and Challenges

A canal or channel is an artificial or natural waterway designed to convey water for purposes such as irrigation, drainage, navigation, or flood control. While channels may be natural or engineered, canals are typically man-made and lined or shaped for controlled flow.

---

📚 Types of Canals and Channels

Type	Description
Irrigation Canal	Delivers water to agricultural fields
Drainage Channel	Removes excess water from land or urban areas
Navigation Canal	Designed for boat or ship movement
Flood Control Channel	Manages stormwater and prevents urban flooding
Natural Channel	Formed by geomorphic processes; irregular cross-section
Engineered Channel	Designed with specific geometry (e.g., trapezoidal, rectangular)

---

📐 Design Methods

Method	Description
Manning’s Equation	Used to size channels based on flow, slope, and roughness
Tractive Force Method	Ensures bed stability by limiting shear stress
Permissible Velocity Method	Limits erosion by controlling flow velocity
Empirical Formulas	Region-specific design charts and regression models
Optimization Models	Used for cost-effective lining and cross-section design

---

📐 Major Design Criteria for Channel Design

Channel design varies by purpose — irrigation, drainage, flood control, navigation — but all require careful consideration of hydraulic, structural, and environmental factors.

---

✅ General Design Criteria

Criterion	Description
Flow Capacity	Must convey design discharge without overtopping or excessive velocity
Hydraulic Efficiency	Minimize energy loss; optimize cross-section for uniform flow
Stability	Prevent erosion, sedimentation, and bank failure
Freeboard	Vertical buffer above water surface to prevent overflow
Slope and Geometry	Ensure self-cleansing velocity and structural integrity
Lining Material	Selected based on erosion resistance, cost, and maintenance needs
Accessibility	Allow for inspection, cleaning, and repairs
Environmental Impact	Minimize disruption to habitats and natural flow regimes

---

📊 Design Criteria by Channel Type

Channel Type	Key Design Criteria
Irrigation Channel	- Uniform flow for equitable distribution - Minimize seepage losses - Gentle slope for control
Drainage Channel	- Rapid removal of excess water - Erosion control - Adequate capacity during storms
Flood Control Channel	- Convey peak flows safely - High freeboard - Energy dissipation structures
Navigation Canal	- Sufficient depth and width for vessels - Stable banks - Controlled velocity
Natural Channel Restoration	- Mimic natural morphology - Support habitat - Manage sediment transport

---

⚠️ Channel Failure History in the U.S.

This table summarizes notable types of channel failures in the U.S., including causes, impacts, and lessons learned. These failures often involve engineered flood control channels, irrigation canals, and urban drainage systems.

Location / Project	Year	Channel Type	Failure Cause	Impact / Notes
Los Angeles River (CA)	Various	Concrete flood channel	Sediment buildup, poor maintenance	Reduced capacity; localized flooding
Central Arizona Project	1993	Irrigation canal	Bank erosion, overtopping	Crop damage; canal breach
New Orleans (LA)	2005	Drainage canals	Levee and floodwall failure (Katrina)	Catastrophic urban flooding; major infrastructure loss
Teton Dam (ID)	1976	Reservoir outlet channel	Structural collapse of dam	Massive downstream flooding; 11 fatalities
San Antonio River (TX)	1998	Urban channel	Inadequate conveyance during storm	Flash flooding; infrastructure overwhelmed
Sacramento River (CA)	Ongoing	Natural channel	Bank erosion, sedimentation	Habitat degradation; flood risk
Imperial Valley (CA)	1905	Irrigation canal	Colorado River diversion failure	Created Salton Sea; long-term ecological impact

---

🔍 Common Failure Mechanisms

• Hydraulic Overload: Flow exceeds design capacity

• Bank Instability: Erosion, piping, or slope failure

• Sediment Accumulation: Reduces conveyance and alters flow paths

• Structural Defects: Cracks, joint failures, or poor construction

• Poor Maintenance: Vegetation, debris, or neglected repairs

• Extreme Events: Hurricanes, flash floods, or seismic activity

---

⚠️ Design Challenges

Challenge	Description
Erosion and Sedimentation	Unlined channels may erode or silt up over time
Vegetation Growth	Can obstruct flow and reduce capacity
Structural Stability	Requires proper slope and lining to prevent collapse
Hydraulic Efficiency	Balancing flow capacity with energy losses
Maintenance Access	Channels must be accessible for cleaning and repairs
Environmental Impact	May alter natural flow regimes and aquatic habitats

---

🧠 Conceptual Insight

Channels and canals are the arteries of water infrastructure —
their design must balance hydraulic performance, environmental sustainability,
and long-term stability under varying flow conditions.

Channel failures often result from a combination of hydraulic misestimation, geotechnical instability, and maintenance neglect.
Understanding past failures helps improve resilience, design standards, and emergency preparedness.

Channel design is a multi-objective process — balancing hydraulic performance,
structural stability, ecological integrity, and long-term sustainability.

---

❓ Quiz Questions

Both [Gupta, 2017] and [Chanson, 2004]channel design particularly in the context of open channel flow. [Gupta, 2017] typically introduces Kennedy’s and Lacey’s theories for alluvial channel design, focusing on sediment transport and stability. The book provides a formula-driven and exam-oriented approach, ideal for undergraduate learners and competitive exams. [Chow, 1959] also provides foundational theory on hydraulic jumps as energy dissipators including subsequent depth, energy loss, and focus on analytical derivation, whereas [Chanson, 2004] offers an advanced design method for different types of spillways and emphasizes experimental data and modern hydraulics.

2. Simulation

🌊 Theoretical Background: Interactive Canal Design Tool

This tool supports the design of open channels for irrigation, drainage, or conveyance systems. It allows users to select between rigid channels (lined or stable) and mobile channels (self-formed in alluvial soils), and accounts for whether the flow is sediment-free or sediment-laden.

---

📘 Design Methodologies

1. Manning’s Equation (Rigid Channel, Sediment-Free)

Used to estimate uniform flow velocity:

\[ V = \frac{1}{n} R^{2/3} S^{1/2} \quad \text{and} \quad Q = A \cdot V \]

• \(( V \)): velocity (m/s)

• \(( Q \)): discharge (m³/s)

• \(( A \)): cross-sectional area (m²)

• \(( R \)): hydraulic radius (m)

• \(( S \)): slope (m/m)

• \(( n \)): Manning’s roughness coefficient

---

2. Tractive Stress Analysis (Rigid Channel, Sediment-Laden)

Used to ensure flow velocity avoids siltation and erosion:

\[ \tau = \gamma R S \]

• \(( \tau \)): tractive stress (N/m²)

• \(( \gamma \)): unit weight of water (typically 9800 N/m³)

• \(( R \)): hydraulic radius

• \(( S \)): slope

Design checks:

• Minimum velocity to prevent sediment deposition

• Maximum velocity to prevent boundary erosion

---

3. Kennedy’s Method (Mobile Channel)

Empirical method for designing stable channels in alluvial soils:

\[ V = 0.55 \cdot y^{0.64} \cdot m^{0.33} \]

• \(( V \)): non-silting velocity (m/s)

• \(( y \)): flow depth (m)

• \(( m \)): silt factor (depends on sediment size)

---

4. Lacey’s Method (Mobile Channel)

Used for designing channels in regime conditions:

\[ V = 0.48 \cdot \left( \frac{Q}{f} \right)^{1/6} \]

• \(( V \)): regime velocity (m/s)

• \(( Q \)): discharge (m³/s)

• \(( f \)): silt factor (depends on sediment size and type)

---

📐 Geometry and Flow Parameters

• Bottom Width (b): width of channel bed (m)

• Flow Depth (y): vertical depth of water (m)

• Slope (S): bed slope (m/m)

• Discharge (Q): flow rate (m³/s)

• Manning’s n: roughness coefficient (typical range 0.012–0.035)

• Silt Factor (m, f): empirical values based on sediment type

---

📊 Stability Criteria

Parameter	Typical Range
Manning’s n	0.012–0.035
Slope (S)	0.0001–0.01

import numpy as np
import ipywidgets as widgets
from IPython.display import display, clear_output

# Constants
g = 9.81  # gravity (m/s²)

# Manning's equation
def mannings(Q=None, n=0.015, A=None, R=None, S=None):
    if Q is None:
        return (1/n) * A * R**(2/3) * S**0.5
    else:
        return Q / (A * R**(2/3) * S**0.5)

# Tractive stress analysis
def tractive_stress(gamma, R, S):
    return gamma * R * S  # N/m²

# Kennedy's method (simplified)
def kennedy_velocity(m, y):
    return 0.55 * y**0.64 * m**0.33

# Lacey's method (simplified)
def lacey_velocity(Q, f):
    return 0.48 * (Q / f)**(1/6)

# Widgets
channel_type = widgets.Dropdown(options=["Rigid", "Mobile"], description="Channel Type")
flow_type = widgets.Dropdown(options=["Sediment-Free", "Sediment-Laden"], description="Flow Type")

b_slider = widgets.FloatSlider(value=3.0, min=1.0, max=10.0, step=0.5, description="Bottom Width (m)")
y_slider = widgets.FloatSlider(value=1.0, min=0.5, max=5.0, step=0.1, description="Flow Depth (m)")
n_slider = widgets.FloatSlider(value=0.015, min=0.010, max=0.035, step=0.001, description="Manning's n")
S_slider = widgets.FloatSlider(value=0.001, min=0.0001, max=0.01, step=0.0001, description="Slope (m/m)")
Q_slider = widgets.FloatSlider(value=5.0, min=1.0, max=50.0, step=1.0, description="Discharge (m³/s)")
gamma_slider = widgets.FloatSlider(value=9800, min=9000, max=10000, step=100, description="Unit Weight (N/m³)")
v_min_slider = widgets.FloatSlider(value=0.3, min=0.2, max=1.0, step=0.05, description="Min Velocity (m/s)")
v_max_slider = widgets.FloatSlider(value=2.0, min=1.0, max=3.0, step=0.1, description="Max Velocity (m/s)")
m_slider = widgets.FloatSlider(value=1.0, min=0.5, max=2.0, step=0.1, description="Kennedy's m")
f_slider = widgets.FloatSlider(value=1.0, min=0.5, max=2.5, step=0.1, description="Lacey's f")

output = widgets.Output()
run_button = widgets.Button(description="Run Design", button_style='success')

# Design function
def run_design(button=None):
    with output:
        clear_output()
        b = b_slider.value
        y = y_slider.value
        n = n_slider.value
        S = S_slider.value
        Q = Q_slider.value
        gamma = gamma_slider.value
        v_min = v_min_slider.value
        v_max = v_max_slider.value
        m = m_slider.value
        f = f_slider.value

        A = b * y
        P = b + 2 * y
        R = A / P

        print(f"📐 Cross-sectional Area: {A:.2f} m²")
        print(f"📏 Hydraulic Radius: {R:.2f} m")

        if channel_type.value == "Rigid":
            print(f"\n🧱 Rigid Channel Design ({flow_type.value})")
            V = mannings(n=n, A=A, R=R, S=S)
            print(f"🔄 Manning's Velocity: {V:.2f} m/s")
            Q_calc = V * A
            print(f"💧 Discharge: {Q_calc:.2f} m³/s")

            if flow_type.value == "Sediment-Laden":
                print(f"\n🧪 Tractive Stress Analysis")
                tau = tractive_stress(gamma, R, S)
                print(f"🧲 Tractive Stress: {tau:.2f} N/m²")
                if V < v_min:
                    print("⚠️ Velocity too low — risk of siltation.")
                elif V > v_max:
                    print("⚠️ Velocity too high — risk of erosion.")
                else:
                    print("✅ Velocity within safe range.")

        elif channel_type.value == "Mobile":
            print(f"\n🌿 Mobile Channel Design ({flow_type.value})")
            V_k = kennedy_velocity(m, y)
            V_l = lacey_velocity(Q, f)
            print(f"🔄 Kennedy's Velocity: {V_k:.2f} m/s")
            print(f"🔄 Lacey's Velocity: {V_l:.2f} m/s")
            print("✅ Use these velocities to guide channel geometry and stability.")

# Visibility function
def update_visibility(change=None):
    with output:
        clear_output()
        base = [channel_type, flow_type, b_slider, y_slider, S_slider, Q_slider]
        if channel_type.value == "Rigid":
            inputs = base + [n_slider]
            if flow_type.value == "Sediment-Laden":
                inputs += [gamma_slider, v_min_slider, v_max_slider]
        elif channel_type.value == "Mobile":
            inputs = base + [m_slider, f_slider]
        display(widgets.VBox(inputs + [run_button]))

# Link triggers
channel_type.observe(update_visibility, names='value')
flow_type.observe(update_visibility, names='value')
run_button.on_click(run_design)

# Initial display
update_visibility()
display(output)

3. Simulation

🌊 Interactive Channel Design Method Selector

This tool recommends the most suitable channel design method based on user-defined parameters such as flow rate, channel type, soil condition, erosion risk, and lining material.

---

✅ What the Code Does

Component	Description
Design Recommendation	Suggests a channel design method based on input conditions
Interactive Inputs	Sliders and dropdowns for flow rate, channel type, soil type, erosion risk, and lining
Decision Logic	Uses rule-based conditions to match inputs to appropriate design methods
Output Summary	Displays recommended method and input parameters

---

▶️ How It Works

• Uses ipywidgets.interact to create interactive controls

• Applies conditional logic:

  • Permissible Velocity Method → Sandy soil or high erosion risk

  • Tractive Force Method → Drainage channels with high erosion risk

  • Manning’s Equation → Lined channels or low-risk conditions

  • Energy-Based Design → Flood control with high flow (>100 m³/s)

  • Geomorphic Design → Natural restoration projects

• Displays results dynamically as inputs change

---

📊 How to Interpret the Result

Output Parameter	Meaning
Recommended Method	Most suitable design approach for the given scenario
Input Summary	Confirms flow rate, channel type, soil, erosion risk, and lining
Use Case	Supports preliminary design decisions and educational exploration

---

🧠 Conceptual Insight

This tool helps match hydraulic design methods to site-specific conditions,
promoting safer, more efficient, and context-sensitive channel engineering.

import ipywidgets as widgets
from ipywidgets import interact
from IPython.display import display, clear_output

# 📌 Decision logic for selecting channel design method
def select_design_method(flow_rate, channel_type, soil_type, erosion_risk, lining):
    clear_output(wait=True)

    # Decision rules
    if channel_type == 'Irrigation':
        if soil_type == 'Sandy' or erosion_risk == 'High':
            method = "Permissible Velocity Method"
            reason = "Sandy soils and high erosion risk require velocity control to prevent channel degradation."
        elif lining == 'Concrete':
            method = "Manning’s Equation with Lined Channel Assumptions"
            reason = "Concrete lining allows for efficient flow estimation using Manning’s equation."
        else:
            method = "Empirical Design Charts (e.g., USBR)"
            reason = "Empirical charts are suitable for irrigation channels with moderate risk and unlined sections."
    elif channel_type == 'Drainage':
        if erosion_risk == 'High':
            method = "Tractive Force Method"
            reason = "High erosion risk in drainage channels requires shear stress control to maintain stability."
        else:
            method = "Manning’s Equation with Freeboard Consideration"
            reason = "Moderate risk allows for standard hydraulic design with added freeboard for safety."
    elif channel_type == 'Flood Control':
        if flow_rate > 100:
            method = "Energy-Based Design with Backwater Analysis"
            reason = "High flows demand energy-grade line analysis to prevent flooding and ensure conveyance."
        else:
            method = "Manning’s Equation with Safety Factor"
            reason = "Lower flows can be managed with conventional design and conservative safety margins."
    elif channel_type == 'Natural Restoration':
        method = "Geomorphic Channel Design / Rosgen Classification"
        reason = "Restoration projects aim to mimic natural morphology and support ecological function."
    else:
        method = "Consult regional standards or hydraulic modeling tools"
        reason = "Input combination is outside standard rules; refer to local guidelines or modeling software."

    # 📋 Output
    print(f"🌊 Recommended Design Method: {method}")
    print(f"📌 Based on:")
    print(f" - Flow Rate: {flow_rate} m³/s")
    print(f" - Channel Type: {channel_type}")
    print(f" - Soil Type: {soil_type}")
    print(f" - Erosion Risk: {erosion_risk}")
    print(f" - Lining Material: {lining}")
    print("\n🔍 Interpretation:")
    print(f" - {reason}")

# 🎛️ Interactive controls
interact(select_design_method,
         flow_rate=widgets.FloatSlider(value=50, min=1, max=500, step=5, description='Flow Rate (m³/s)'),
         channel_type=widgets.Dropdown(options=['Irrigation', 'Drainage', 'Flood Control', 'Natural Restoration'], description='Channel Type'),
         soil_type=widgets.Dropdown(options=['Clay', 'Silt', 'Sandy', 'Gravel'], description='Soil Type'),
         erosion_risk=widgets.Dropdown(options=['Low', 'Moderate', 'High'], description='Erosion Risk'),
         lining=widgets.Dropdown(options=['None', 'Concrete', 'Riprap', 'Vegetated'], description='Lining Material'));

4. Self-Assessment

🧠 Canal Design Knowledge Check

This section includes quiz-style questions to test understanding, conceptual questions to deepen insight, and reflective prompts to encourage design thinking.

---

❓ Quiz Questions

Multiple Choice

1. Which parameter most directly affects tractive stress in a channel?
   A. Flow depth
   B. Slope
   C. Bottom width
   D. Manning’s n
   Answer: B

2. Kennedy’s method is primarily used for:
   A. Concrete-lined channels
   B. Sediment-free flow
   C. Mobile channels in alluvium
   D. Urban stormwater drains
   Answer: C

3. Lacey’s regime velocity increases with:
   A. Decreasing discharge
   B. Increasing silt factor
   C. Increasing slope
   D. Increasing discharge
   Answer: D

True/False

4. Manning’s equation assumes uniform flow.
   Answer: True

5. Tractive stress is higher in channels with steep slopes.
   Answer: True

6. Kennedy’s method accounts for sediment size via the silt factor.
   Answer: True

---

📘 Conceptual Questions

1. Why is hydraulic radius a more reliable indicator of flow efficiency than flow depth alone?

2. How does sediment-laden flow influence the design constraints of a rigid channel?

3. What are the limitations of using empirical methods like Kennedy’s and Lacey’s for mobile channel design?

4. Why is it important to define both minimum and maximum allowable velocities in sediment-laden flow?

5. How does Manning’s roughness coefficient vary with channel lining and vegetation?

---

🔍 Reflective Questions

1. If you were designing a canal in a mountainous region with high sediment load, which method would you prioritize and why?

2. How would your design change if the goal was to minimize maintenance rather than maximize hydraulic efficiency?

3. What trade-offs exist between using a concrete-lined channel versus a self-formed mobile channel?

4. How could climate change (e.g., increased flow variability) affect the assumptions behind uniform flow design?

5. What additional parameters or models would you include to make this tool more robust for real-world applications?

---