Chapter 2 Hydrology: Habitat Analysis

Chapter 2 Hydrology: Habitat Analysis#

  1. Introduction: Habitat Analysis

  2. Simulation

  3. Self-Assessment

1. Introduction#

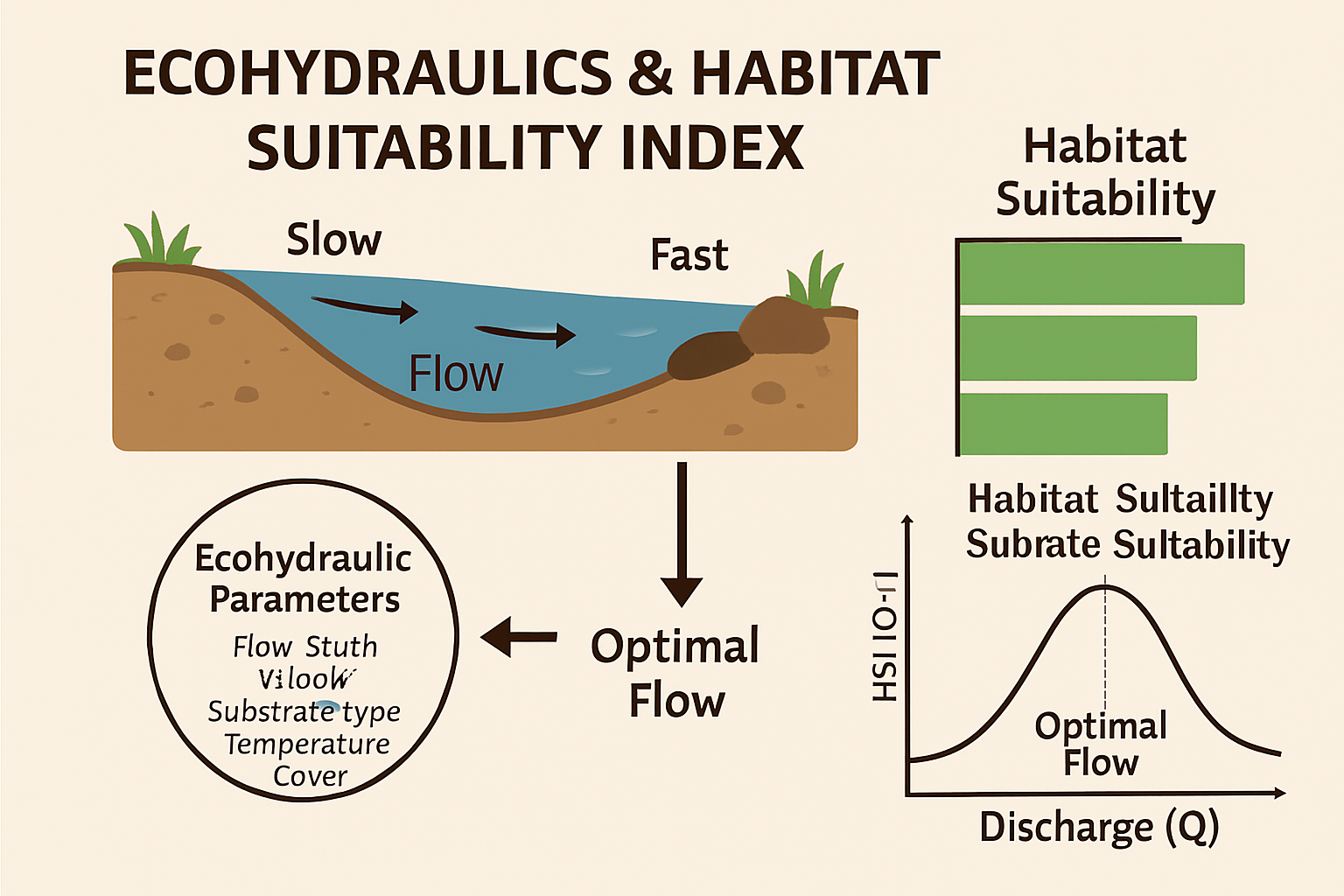
Descriptive alt text for accessibility

Fig. 5 ** Figure 2.5 **: Eco-Hydraulics and Habitat Suitability Index.#

🌿 Habitat Analysis and Hydraulics: Concepts and Methods#

Human interventions like dam construction, channelization, and river regulation aim to reduce natural flow variability for flood control, irrigation, and hydropower. However, these often lead to:

🌊 Ecological Consequences []#

  • Habitat degradation: Loss of riffles, pools, and floodplain connectivity

  • Fragmentation: Barriers to fish migration and gene flow

  • Altered flow regimes: Disruption of seasonal cues for spawning and feeding

  • Thermal pollution: Stratification and cold-water releases downstream

  • Sediment retention: Starvation of downstream habitats and delta erosion

  • Biodiversity loss: Decline in native fish, macroinvertebrates, and aquatic plants

🔹 Habitat Analysis#

The study of physical, biological, and ecological conditions that support species survival, reproduction, and persistence. It involves assessing habitat quality, availability, and suitability for target organisms.

🔹 Hydraulics#

The science of water movement through natural or engineered channels. In habitat studies, it focuses on flow depth, velocity, shear stress, and inundation patterns that shape aquatic environments.

  • Hydraulic conditions define habitat structure: Flow depth, velocity, and substrate interaction determine where species can live, feed, and spawn.

  • Habitat suitability is species-specific: Different species prefer distinct hydraulic niches (e.g., slow shallow water for larvae, fast riffles for adults).

  • Hydraulic modeling enables habitat prediction: Simulations help assess habitat availability under varying flow regimes, especially in regulated rivers.

Over 60% of large rivers are now fragmented by dams, with severe consequences for aquatic biodiversity. Most sttides show negative ecolocial changes in respose to a variety of flow alteration [Poff and Zimmerman, 2010]

🔄 Restoration and Rehabilitation: Purpose and Principles#

Restoration aims to reestablish ecological integrity by improving habitat structure, flow regimes, and connectivity. Rehabilitation may not restore original conditions but seeks to enhance ecosystem function.

🧭 Goals#

  • Restore natural hydrodynamics and sediment transport

  • Reconnect longitudinal and lateral habitats

  • Improve water quality and temperature regimes

  • Support species recovery and recolonization

🛠️ Common Measures#

  • Dam removal or modification (e.g. fish ladders)

  • Environmental flow releases

  • Floodplain reconnection

  • Riparian zone restoration

  • Nature-based solutions (e.g. re-meandering, wetland creation)

⚙️ Key Hydraulic Parameters in Habitat Analysis#

Parameter

Description

Ecological Role

Depth (d)

Vertical distance from water surface to bed

Determines refuge and spawning zones

Velocity (v)

Speed of water flow

Influences feeding and energy use

Shear stress (τ)

Force exerted on bed/bank surfaces

Affects substrate stability and erosion

Discharge (Q)

Volume of flow per unit time

Controls habitat extent and connectivity

Substrate type

Bed material (sand, gravel, cobble)

Affects spawning and benthic habitat

Inundation area

Spatial extent of flow coverage

Defines usable habitat zones

🧪 Methods for Habitat Analysis (Simple to Complex)#

Method

Description

Tools/Models

Complexity

Visual Assessment

Field-based habitat scoring

EPA Rapid Bioassessment

🟢 Simple

Habitat Suitability Index (HSI)

Empirical rating of habitat quality

Field data + GIS

🟡 Moderate

PHABSIM []

Physical Habitat Simulation

Depth, velocity, substrate

🔵 Moderate

2D Hydraulic Modeling

Spatial simulation of flow and habitat

HEC-RAS 2D, SRH-2D

🔴 Advanced

Ecohydraulic Modeling

Integrates hydraulics with species life cycles

Coupled H&H + ecological models

🔴 Advanced

Habitat Connectivity Models

Graph/network-based analysis

GIS + landscape metrics

🔴 Advanced

📈 Practical Applications#

  • Environmental flow design

  • Species conservation planning

  • Stream restoration

  • Impact assessment under NEPA/ESA

  • Adaptive management of regulated rivers

Foundational Literature#

[], [Bovee, 1986], [],[Bovee, 1986] collectively establish the foundation of ecohydraulics and habitat suitability indexing. [Bovee, 1986] introduced Habitat Suitability Criteria within IFIM, providing a structured approach to assess ecological responses to flow. [] enhanced PHABSIM by linking hydraulic simulations to biological needs through Weighted Usable Area. [] offered critical hydrologic and geomorphic context, while [] advanced fish passage modeling using applied hydraulics. Together, these studies integrate physical river processes with ecological criteria, enabling sustainable flow management and informed habitat assessments.

Methodology: 1D Hydraulic Habitat Suitability Model#

This model estimates fish habitat suitability based on discharge, channel geometry, and slope using a simplified 1D hydraulic approach. It integrates hydraulic calculations with species-specific habitat preferences to evaluate habitat quality and usable area.

Overview#

The model simulates:

  • Channel hydraulics using Manning’s equation

  • Depth and velocity at a given discharge and slope

  • Habitat Suitability Index (HSI) for depth and velocity

  • Combined HSI using geometric mean

  • Usable habitat area per unit stream length

It supports interactive scenario testing for different species and flow conditions.

Hydraulic Calculations#

Manning’s Equation#

To estimate flow velocity and depth:

\[ Q = A \cdot V \quad ; \quad V = \frac{1}{n} \cdot R^{2/3} \cdot S^{1/2} \quad ; \quad R = \frac{A}{P} \]

Where:

  • \(( Q \)): discharge (m³/s)

  • \(( A \)): cross-sectional area = width × depth

  • \(( V \)): velocity (m/s)

  • \(( R \)): hydraulic radius

  • \(( P \)): wetted perimeter (trapezoidal approximation)

  • \(( S \)): channel slope

  • \(( n \)): Manning’s roughness coefficient (default 0.035)

The model iteratively solves for depth ( d ) that satisfies the target discharge.

Habitat Suitability Index (HSI)#

HSI values range from 0 (unsuitable) to 1 (optimal). They are computed for:

Depth HSI#

\[ HSI_d = \text{clip}\left(1 - \frac{|d - d_{\text{opt}}|}{d_{\text{range}}}, 0, 1\right) \]

Velocity HSI#

\[ HSI_v = \text{clip}\left(1 - \frac{|v - v_{\text{opt}}|}{v_{\text{range}}}, 0, 1\right) \]

Where:

  • \(( d_{\text{opt}} \)), \(( v_{\text{opt}} \)): optimal depth and velocity

  • \(( d_{\text{range}} \)), \(( v_{\text{range}} \)): tolerance ranges

  • Values vary by species (trout, salmon, minnow)

Combined HSI#

\[ HSI_{\text{combined}} = \sqrt{HSI_d \cdot HSI_v} \]

This geometric mean balances depth and velocity suitability.

Usable Habitat Area#

\[ \text{Usable Area} = \text{Channel Width} \cdot HSI_{\text{combined}} \]

This represents the effective habitat width per meter of stream length.

Interpretation Framework#

  • HSI > 0.8 → Excellent habitat

  • HSI 0.5–0.8 → Moderate habitat

  • HSI < 0.5 → Poor habitat

The model compares computed depth and velocity to typical habitat ranges for each species and provides diagnostic feedback.

Applicability#

  • Rapid assessment of habitat quality under varying flow conditions

  • Supports instream flow recommendations and restoration design

  • Useful for educational and scenario-based exploration

Limitations#

  • Assumes trapezoidal channel geometry

  • Simplified 1D hydraulics; no lateral or temporal variation

  • HSI curves are generic and may require calibration

  • Does not include substrate or temperature effects

“This model bridges hydraulic simulation and ecological insight, helping visualize how flow and channel form shape habitat availability for aquatic species.”

2. Simulation#

import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact, FloatSlider, Dropdown

# 📐 Habitat Suitability Index (HSI) functions
def depth_hsi(depth, species='trout'):
    if species == 'trout':
        return np.clip(1 - abs(depth - 0.5) / 0.5, 0, 1)
    elif species == 'salmon':
        return np.clip(1 - abs(depth - 0.8) / 0.6, 0, 1)
    else:  # minnow
        return np.clip(1 - abs(depth - 0.3) / 0.4, 0, 1)

def velocity_hsi(velocity, species='trout'):
    if species == 'trout':
        return np.clip(1 - abs(velocity - 0.4) / 0.4, 0, 1)
    elif species == 'salmon':
        return np.clip(1 - abs(velocity - 0.6) / 0.5, 0, 1)
    else:  # minnow
        return np.clip(1 - abs(velocity - 0.2) / 0.3, 0, 1)

# 📊 Habitat suitability calculation with Manning's equation
def simulate_habitat(Q, width, slope, species):
    g = 9.81
    n = 0.035  # typical roughness for natural streams

    # Estimate depth using Manning's equation (simplified trapezoidal)
    for d in np.linspace(0.1, 5.0, 500):
        A = width * d
        P = width + 2 * np.sqrt(1**2 + d**2)
        R = A / P
        V = (1/n) * R**(2/3) * slope**0.5
        Q_calc = V * A
        if abs(Q_calc - Q) < 0.2:
            depth = d
            velocity = V
            break
    else:
        depth = np.nan
        velocity = np.nan
        print("⚠️ Manning's equation did not converge. Try adjusting slope or discharge.")
        return

    # HSI calculations
    hsi_d = depth_hsi(depth, species)
    hsi_v = velocity_hsi(velocity, species)
    hsi_combined = (hsi_d * hsi_v)**0.5  # geometric mean
    usable_area = width * hsi_combined  # per unit length

    # Typical habitat ranges
    typical_depth = {'trout': (0.3, 0.7), 'salmon': (0.5, 1.2), 'minnow': (0.2, 0.5)}
    typical_velocity = {'trout': (0.2, 0.6), 'salmon': (0.3, 0.8), 'minnow': (0.1, 0.4)}

    # Output summary
    print(f"🌊 Discharge: {Q:.2f} m³/s | Slope: {slope:.4f}")
    print(f"📏 Width: {width:.2f} m | Depth: {depth:.2f} m | Velocity: {velocity:.2f} m/s")
    print(f"🧪 Depth HSI: {hsi_d:.2f} | Velocity HSI: {hsi_v:.2f} | Combined HSI: {hsi_combined:.2f}")
    print(f"🏞️ Usable Habitat Area (per m): {usable_area:.2f} m²")

    # Interpretation
    print("\n🔎 Interpretation:")
    if hsi_combined > 0.8:
        print(f"✅ Excellent habitat conditions for {species}")
    elif hsi_combined > 0.5:
        print(f"🟡 Moderate habitat suitability for {species}")
    else:
        print(f"❌ Poor habitat conditions for {species} — consider flow or channel adjustments")

    print(f"📘 Typical depth range for {species}: {typical_depth[species][0]}–{typical_depth[species][1]} m")
    print(f"📘 Typical velocity range for {species}: {typical_velocity[species][0]}–{typical_velocity[species][1]} m/s")

    # 📈 Visualization
    plt.figure(figsize=(8, 4))
    plt.bar(['Depth HSI', 'Velocity HSI', 'Combined HSI'], [hsi_d, hsi_v, hsi_combined], color='skyblue')
    plt.title(f"Habitat Suitability for {species.capitalize()}")
    plt.ylim(0, 1.1)
    plt.grid(True, linestyle='--', alpha=0.5)
    plt.tight_layout()
    plt.show()

# 🎛️ Interactive controls
interact(
    simulate_habitat,
    Q=FloatSlider(value=5, min=0.1, max=50, step=0.5, description="Discharge Q (m³/s)"),
    width=FloatSlider(value=10, min=2, max=50, step=1, description="Channel Width (m)"),
    slope=FloatSlider(value=0.005, min=0.0001, max=0.05, step=0.0005, description="Slope"),
    species=Dropdown(options=['trout', 'salmon', 'minnow'], value='trout', description="Species")
)

<function __main__.simulate_habitat(Q, width, slope, species)>

3. Self-Assessment#

1D Hydraulic Habitat Suitability Model: Quiz, Conceptual & Reflective Questions#

This module reinforces understanding of the hydraulic and ecological principles behind the habitat suitability model. It supports learning through multiple-choice questions, conceptual prompts, and reflective challenges.

Conceptual Questions#

  1. What does the hydraulic radius ( R ) represent in Manning’s equation?

    • A. The average channel depth

    • B. The ratio of flow area to wetted perimeter

    • C. The slope of the channel

    • D. The roughness coefficient

  2. Why is the geometric mean used to combine depth and velocity HSI values?

    • A. It gives equal weight to both parameters

    • B. It emphasizes the lower suitability value

    • C. It avoids overestimating combined suitability

    • D. All of the above

  3. Which factor most directly increases flow velocity in the model?

    • A. Increasing channel width

    • B. Increasing Manning’s roughness

    • C. Increasing slope

    • D. Increasing depth

  4. What does a combined HSI value of 0.9 indicate?

    • A. Poor habitat conditions

    • B. Moderate suitability

    • C. Excellent habitat quality

    • D. Unusable area

  5. Which assumption is made about channel geometry in this model?

    • A. Circular cross section

    • B. Rectangular channel

    • C. Trapezoidal shape

    • D. Variable slope and width

Interpretation#

  1. Why does the model iterate over depth values to match the target discharge?

  2. How does the channel slope influence both depth and velocity in the simulation?

  3. Why is the usable habitat area calculated as width × combined HSI?

  4. What are the implications of using a fixed roughness coefficient across all species and flows?

  5. How could substrate or temperature be integrated into the HSI framework?

Reflective Questions#

  1. How do hydraulic conditions shape the availability of fish habitat in natural streams?

  2. Why is it important to consider both depth and velocity when evaluating habitat suitability?

  3. What are the limitations of using generic HSI curves for species-specific analysis?

  4. How could this model support restoration planning or environmental flow recommendations?

  5. In what ways could this model be extended to include temporal variability or multi-species interactions?

Design Insight#

“Habitat modeling is not just about hydraulics—it’s about understanding how physical conditions translate into ecological opportunities. This model helps visualize that connection and supports informed decision-making.”

Contents