Chapter 3 Hydraulics: Gravity Dam Design

Contents

Chapter 3 Hydraulics: Gravity Dam Design#

  1. Introduction: Gravity Dam

  2. Simulation: Gravity Dam Design

  3. Self-Assessment

1. Introduction#

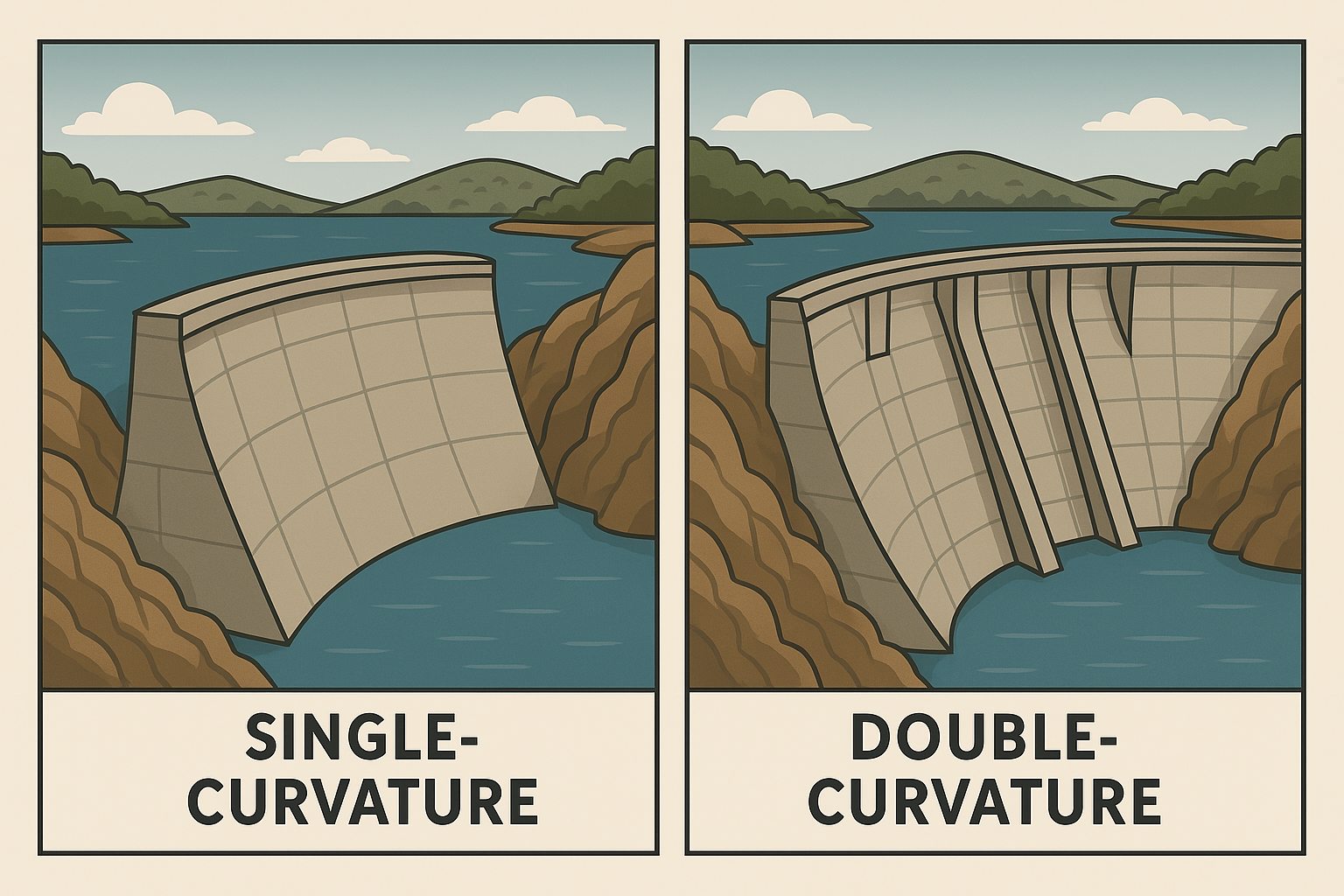
Descriptive alt text for accessibility

Fig. 12 **Figure 3.12 **: Types of Gravity Dam.#

A dam is a hydraulic structure constructed across a river, stream, or watercourse to store, control, or divert water for various purposes. In water resources engineering, dams play a critical role in:

  • Water supply for domestic, agricultural, and industrial use

  • Flood control by regulating downstream flow

  • Hydropower generation through controlled release of water

  • Irrigation by maintaining reservoir levels

  • Navigation by stabilizing river flow

  • Recreation and ecosystem support

Dams are designed to withstand hydraulic, structural, and environmental loads, and their type and configuration depend on site topography, geology, hydrology, and intended function.

📌 Dam classification#

Dams can be classified based on several criteria

🔹 By Hydraulic Design#

  • Overflow dams: e.g., concrete dams that allow water to spill over.

  • Non-overflow dams: e.g., embankment dams that retain water without overtopping.

🔹 By Structural Design#

  • Gravity Dam - Relies on its own weight to resist water pressure. - Typically made of concrete or masonry. - Suitable for wide valleys with strong foundations. Gravity Dams depend on weight for stability against overturning, sliding, and crushing.

  • Optimization involves:

    • Using ¼ to ⅓ of concrete volume to counter uplift.

    • ¾ to ⅔ volume for resisting overturning and shear.

    • Inclined upstream face can improve stress distribution.

  • Hollow gravity dams are lighter alternatives with similar design principles.

-Arch Dam- Curved upstream to transfer loads to abutments. - Requires strong, stable rock walls. - Economical in narrow, steep-sided valleys.

  • Components: - Arch unit: bounded by horizontal planes - Cantilever unit: bounded by vertical radial planes - Extrados: upstream face- Intrados: downstream face

  • Advantages: - Material-efficient and cheaper - Minor uplift issues due to narrow base - Can be built on moderate foundations

  • Disadvantages: - Require strong rock abutments - Specialized design and slow construction - Skilled labor and complex formwork needed

Buttress Dam - Consists of a sloping deck supported by buttresses. - Uses less material than gravity dams. - Suitable for moderate foundations and wider valleys. Buttress Dam require less concrete than gravity dams.

  • Advantages: - Efficient heat dissipation → faster construction - Safer against overturning/sliding due to inclined face- Better stress distribution on foundation - Suitable for weaker foundations

  • Disadvantages: - Require more reinforcement and skilled labor - Expensive formwork - High stress on slabs/columns → potential deterioration

🔹 By Usage#

  • Storage dams: Retain water for supply and regulation.

  • Diversion dams: Redirect flow for irrigation or hydropower.

  • Detention dams: Temporarily store floodwater.

🔹 By Construction Material#

  • Concrete or masonry dams

  • Earth-fill dams

  • Rock-fill dams

  • Earth and rock-fill dams

  • Concrete-faced rock-fill dams (CFRD)

🔹 By Capacity#

  • Small, Medium, or Large dams

🧭 Site Selection Guidance#

✅ Gravity Dam#

  • Topography: Wide valley with ample space.

  • Foundation: Strong rock capable of bearing high loads.

  • Material Availability: Abundant concrete or masonry.

  • Hydrology: Suitable for high water pressure and large reservoirs.

✅ Arch Dam#

  • Topography: Narrow, V-shaped valley with steep rock abutments.

  • Foundation: Extremely strong and stable rock.

  • Material Availability: Less concrete needed.

  • Hydrology: Ideal for deep reservoirs with high head.

✅ Buttress Dam#

  • Topography: Moderate width valleys with gentle slopes.

  • Foundation: Fair to good bearing capacity.

  • Material Availability: Can use reinforced concrete or precast elements.

  • Hydrology: Suitable for medium head and moderate reservoir size.

🌍 Advantages and Disadvantages of Dams#

✅ Advantages#

  • Water regulation: Seasonal and spatial control of water distribution

  • Flood protection: Acts as buffer during heavy rainfall

  • Drought mitigation: Stores excess water for dry periods

  • Sediment control: Reduces downstream sedimentation

❌ Disadvantages#

  • Environmental impact:

    • Alters local climate and precipitation patterns

    • Disrupts ecosystems and terrain

  • Social risks:

    • Poor design or maintenance can endanger lives and infrastructure

    • Potential displacement of communities

📊 Comparative Table of Dam Types#

Dam Type

Structural Principle

Material Use

Foundation Requirement

Topography Suitability

Advantages

Limitations

Gravity Dam

Resists water pressure by weight

High (concrete/masonry)

Very strong and stable rock

Wide valleys

Simple design, durable

Expensive, heavy structure

Arch Dam

Transfers load to abutments via arch

Low

Strong abutments and rock walls

Narrow, steep-sided valleys

Material-efficient, elegant structure

Requires precise geology and construction

Buttress Dam

Sloping deck supported by buttresses

Moderate

Moderate to good foundation

Broad valleys with moderate slopes

Economical, less material than gravity

Complex design, maintenance-intensive

🧱 Gravity Dams and Dam Overview in the U.S.#

A gravity dam is a solid structure (typically concrete or masonry) that resists water pressure by its own weight.

🔧 Design Philosophy#

  • Stability through mass and geometry; Requires strong rock foundation

  • Triangular cross-section; straight or curved plan; Designed for uplift, water pressure, seismic loads

🧠 Modern Design Philosophy#

  • Sediment Management: Include low-level outlets

  • Perpetual Use: Design for long-term sustainability

  • RESCON Model: World Bank framework for sediment economics

✅ Advantages#

- High resistance to overtopping - Long lifespan (>100 years) - Suitable for narrow valleys

❌ Disadvantages#

- High construction cost - Sensitive to uplift pressure - Requires extensive foundation preparation

🏗️ Types of Dams#

Type

Description

Example

Gravity Dam

Resists water by weight

Hoover Dam

Arch Dam

Curved upstream; transfers load to abutments

Glen Canyon Dam

Buttress Dam

Thin slab supported by buttresses

Coolidge Dam

Embankment Dam

Earth or rockfill; relies on mass

Oroville Dam

Diversion Dam

Redirects flow to canals or tunnels

Granite Reef Dam

Cofferdam

Temporary dam for construction

Bridge foundations

Hydropower Dam

Generates electricity

Grand Coulee Dam

🏞️ Dam Design and Considerations#

🧭 Factors Influencing Dam Type#

The choice of dam structure depends on several parameters:

  • Topography:

    • U-shaped rocky valleys → Concrete dams

    • V-shaped valleys → Arch dams

    • Flat plains → Earth-fill dams

  • Geology & Foundation: Must support dam weight; foundations range from solid rock to clay.

  • Material Availability

  • Spillway Design: Size and location are critical.

⚖️ Structural Loads on Gravity Dams#

  • Primary Loads:

    • Water pressure

    • Dam weight

    • Uplift pressure

  • Secondary Loads:

    • Silt pressure

    • Wave pressure

    • Ice pressure

    • Thermal effects

    • Dam-foundation interaction

  • Exceptional Loads:

    • Earthquakes and other rare events

🧪 Material and Foundation Considerations

  • Concrete properties: Strength, elasticity, thermal and dynamic behavior.

  • Foundation: Rock-based assumptions, with detailed geotechnical investigations and in-situ testing.

  • Grouting and joints: Guidelines for contraction joints, galleries, and seepage control.

🌿 Environmental and Ecological Considerations

  • Impact on fish and wildlife

  • Reservoir-induced changes to ecosystems

  • Cultural and recreational values

  • Site selection based on minimizing ecological disruption

📐 Design Layout and Appurtenances

  • Spillways, non-overflow sections, freeboard, and drainage galleries.

  • Temperature control during construction to prevent cracking.

  • Instrumentation for monitoring dam behavior post-construction.

📊 Safety and Performance

  • Factors of safety for sliding, cracking, and foundation stability.

  • Loading combinations: Usual, unusual, and extreme scenarios.

  • Performance monitoring: Emphasized for long-term dam integrity.

🏞️ Major Dams in the U.S.#

Dam Name

Type

Height (ft)

River

State

Oroville Dam

Embankment

770

Feather River

California

Hoover Dam

Gravity/Arch

726

Colorado River

NV/AZ

Grand Coulee Dam

Gravity

550

Columbia River

Washington

Glen Canyon Dam

Arch

710

Colorado River

Arizona

Dworshak Dam

Gravity

717

Clearwater River

Idaho

💥 Notable Dam Failures in the U.S.#

Event

Year

Location

Fatalities

Cause

South Fork Dam

1889

Johnstown, PA

2,209

Poor maintenance, heavy rain

St. Francis Dam

1928

California

~450

Foundation failure

Teton Dam

1976

Idaho

11

Piping/internal erosion

Kelly Barnes Dam

1977

Georgia

39

Rainfall, structural issues

Edenville Dam

2020

Michigan

0

Structural failure, oversight

🗺️ Dam Distribution in the U.S. [U.S. Army Corps of Engineers, 2025]#

🧱 Gravity Dam Stability Analysis – Summary Table#

This table summarizes the key checks for gravity dam stability: sliding, overturning, and stress failure, including governing equations and force/moment components.

Stability Check

Governing Equation / Criterion

Forces Considered

Moment Calculation / Notes

Sliding

\(( F_s = \frac{R}{H} \geq \text{Safety Factor} \))

- \(( R \)): resisting force (friction + cohesion)
- \(( H \)): horizontal driving force (water pressure, uplift)

No moment; force balance along horizontal direction

\(( R = W \cdot \tan(\phi) + c \cdot A \))

- \(( W \)): weight of dam
- \(( \phi \)): friction angle
- \(( c \)): cohesion
- \(( A \)): base area

Safety factor typically ≥ 1.5

Overturning

\(( \frac{M_R}{M_O} \geq \text{Safety Factor} \))

- \(( M_R \)): resisting moment (due to dam weight)
- \(( M_O \)): overturning moment (due to water pressure, uplift)

Moments taken about toe of dam

\(( M_R = W \cdot \frac{b}{2} \))

- \(( b \)): base width

Safety factor typically ≥ 2.0

\(( M_O = P \cdot \frac{h}{3} \))

- \(( P \)): hydrostatic force
- \(( h \)): water height

Includes uplift moment if applicable

Stress Failure

\(( \sigma = \frac{P}{A} \pm \frac{M}{Z} \))

- \(( \sigma \)): normal stress
- \(( P \)): vertical load
- \(( M \)): moment
- \(( Z \)): section modulus

Check for tensile stress at heel or toe

\(( Z = \frac{b^2}{6} \)) (for rectangular section)

- \(( A = b \cdot 1 \)) (unit length)

Ensure compressive stress < allowable stress

Check: \(( \sigma_{\text{max}} \leq \sigma_{\text{allow}} \))

- Include uplift pressure reduction

No tension allowed at base (gravity dams)

🧠 Notes#

  • Uplift Pressure: Reduces effective weight and adds to sliding/overturning forces.

  • Safety Factors: Typically ≥ 1.5 for sliding, ≥ 2.0 for overturning, and stress within material limits.

  • Load Combinations: Include dead load, hydrostatic pressure, uplift, silt, ice, and seismic forces.

🧠 Conceptual Insight#

Dams are critical infrastructure for water storage, flood control, hydropower, and ecosystem management.
Understanding dam types, design philosophy, and historical failures helps improve future resilience and safety.

References#

-[United States Bureau of Reclamation, 1976]- Serves as a technical guide for designing concrete gravity dams of all heights (except those under 50 feet, which are addressed in Design of Small Dams). The book emphasizes sound engineering practices, safety, and environmental stewardship. The design principle encompasses 1) stability requirements (against overturning, sliding, and foundation failure), 2) various load types (dead load, hydrostatic, uplift, and silt), and 3) analysis methods (Gravity, trial-load, and finite element method).

-[United States Bureau of Reclamation, 1976]emphasizes empirical design based on historical Bureau practices, focusing on static stability checks and construction detailing. In contrast, [U.S. Army Corps of Engineers, 1995] manual adopts a more analytical and performance-based approach, integrating dynamic analysis, reevaluation of existing dams, and modern computational tools. While both assume rock foundations and cover sliding, overturning, and stress checks, USACE provides deeper guidance on seismic response and uplift modeling.[Novak et al., 2007] provides a comprehensive and engineering-focused treatment of gravity dam design, covering structural stability, uplift pressure, seepage control, and modern safety considerations.

2. Simulation#

Geometry Inputs#

  • Dam Height (H): vertical height of the dam (m)

  • Bottom Width: width of dam base at foundation (m)

  • Top Width: width at dam crest (m)

  • Drain Location: horizontal distance from upstream toe (m) — helps reduce uplift pressure beneath dam

Uplift Pressure Adjustment#

Drainage gallery modifies uplift distribution:

  • From full hydrostatic pressure at upstream toe

  • To partial pressure at drain

  • Tapering to tailwater pressure at downstream

This yields:

  • Modified uplift force

  • Updated moment due to uplift

Forces Considered#

Force Type

Direction

Description

Dam Weight

Vertical ↓

Gravity from dam mass (concrete)

Hydrostatic Load

Horizontal →

Upstream water pressure

Sediment Load

Horizontal →

Pressure from deposited sediments

Tailwater Load

Horizontal ←

Downstream water pressure (resisting)

Ice & Wave Loads

Horizontal →

Surface impacts due to environmental effects

Uplift Pressure

Vertical ↑

Reduced by drain gallery

Stability Computations#

  • Sliding Factor of Safety (FS)

\[ \text{FS}_{\text{sliding}} = \frac{\text{resisting shear}}{\text{horizontal load}} \]

  • Overturning Factor of Safety (FS)

\[ \text{FS}_{\text{overturning}} = \frac{\text{resisting moment} - \text{uplift moment}}{\text{overturning moment}} \]

  • Toe Stress
    Max base pressure estimated for structural integrity.

Visual Dashboard#

  • Subplot 1: Trapezoidal dam profile with vertical line showing drain position

  • Subplot 2: Bar chart of external force magnitudes (kN/m)

  • Subplot 3: Pie chart of overturning moment contributions from each component

Output Summary#

The script prints:

  • Self-weight of dam - Uplift force (adjusted by drain) - Total horizontal force

  • FS against sliding and overturning - Max toe stress with a safe/overstressed label

To run the simulation, place this code in a Jupyter notebook cell and use sliders to explore how dam dimensions and drainage position impact structural performance 💧📐🧱.

Gravity Dam Load Equations — Force and Moment Calculations#

This section outlines the governing equations used to compute all external forces and moments in the interactive gravity dam model, including effects of a drainage gallery that reduces uplift pressure.

1. Dam Geometry and Self-Weight#

  • Trapezoidal Area:

\[ A_{\text{dam}} = H \cdot \frac{B_{\text{bottom}} + B_{\text{top}}}{2} \]

  • Weight (Force):

\[ W_{\text{dam}} = \gamma_c \cdot A_{\text{dam}} \quad \text{[kN/m]} \]

  • Centroid (Moment Arm from Toe):

\[ x_W = \frac{B_{\text{bottom}}^2 + 2B_{\text{bottom}}B_{\text{top}} + B_{\text{top}}^2}{3(B_{\text{bottom}} + B_{\text{top}})} \]

2. Hydrostatic Water Pressure (Upstream)#

  • Force:

\[ P_{\text{upstream}} = \frac{1}{2} \cdot \gamma_w \cdot (H - \text{freeboard})^2 \]

  • Moment Arm:

\[ x_{\text{upstream}} = \frac{H - \text{freeboard}}{3} \]

3. Sediment Pressure#

  • Force:

\[ P_{\text{sediment}} = \frac{1}{2} \cdot \gamma_s \cdot (H - \text{freeboard})^2 \]

  • Moment Arm:

\[ x_{\text{sed}} = \frac{H - \text{freeboard}}{3} \]

4. Tailwater Pressure (Downstream)#

  • Assumed Tailwater Height:

\[ H_{\text{dw}} = \frac{H}{3} \]

  • Force:

\[ P_{\text{tail}} = \frac{1}{2} \cdot \gamma_w \cdot H_{\text{dw}}^2 \]

  • Moment Arm:

\[ x_{\text{tail}} = \frac{H_{\text{dw}}}{3} \]

5. Wave and Ice Loads#

  • Wave Force:

\[ P_{\text{wave}} = \text{wave pressure} \cdot (H - \text{freeboard}) \quad ; \quad x_{\text{wave}} = \frac{H - \text{freeboard}}{2} \]

  • Ice Force:

\[ P_{\text{ice}} = \text{ice pressure} \cdot (H - \text{freeboard}) \quad ; \quad x_{\text{ice}} = \frac{H - \text{freeboard}}{2} \]

6. Uplift Pressure (Adjusted by Drain Location)#

Let ( d ) be the drainage location (from upstream toe), and ( B ) the base width.

  • Upstream Pressure at Toe:

\[ h_{\text{up}} = \gamma_w \cdot (H - \text{freeboard}) \]

  • Downstream Pressure at Toe:

\[ h_{\text{dw}} = \gamma_w \cdot H_{\text{dw}} \]

  • Zone 1 (0 to d):

\[ P_1 = \frac{1}{2} \cdot \left(h_{\text{up}} + h_{\text{up}} \cdot \left(1 - \frac{d}{B}\right) \right) \cdot d \quad ; \quad x_1 = \frac{d}{2} \]

  • Zone 2 (d to B):

\[ P_2 = \frac{1}{2} \cdot \left(h_{\text{up}} \cdot \left(1 - \frac{d}{B}\right) + h_{\text{dw}} \right) \cdot (B - d) \quad ; \quad x_2 = d + \frac{B - d}{2} \]

  • Total Uplift Force & Moment:

\[ \text{Uplift Force} = P_1 + P_2 \quad ; \quad M_{\text{uplift}} = P_1 \cdot x_1 + P_2 \cdot x_2 \]

7. Stability Factors#

  • Sliding Safety Factor:

\[ \text{FS}_{\text{sliding}} = \frac{R_{\text{vert}} \cdot \tan(\phi) + c \cdot B}{P_{\text{horizontal}}} \quad \text{where } R_{\text{vert}} = W_{\text{dam}} - \text{uplift force} \]

  • Overturning Safety Factor:

\[ \text{FS}_{\text{overturning}} = \frac{M_{\text{resisting}} - M_{\text{uplift}}}{M_{\text{overturning}}} \]

  • Toe Stress Estimate:

\[ \text{Stress}_{\text{max}} = \frac{2 R_{\text{vert}}}{B} \quad ; \quad \text{Stress}_{\text{avg}} = \frac{R_{\text{vert}}}{B} \]
import numpy as np
import matplotlib.pyplot as plt
import ipywidgets as widgets
from IPython.display import display

# 🌊 Adjust uplift based on drainage gallery location
def adjusted_uplift(B, H_eff, H_dw, gamma_w, drain_pos):
    h_up = gamma_w * H_eff
    h_dw = gamma_w * H_dw
    
    # Split base into two regions: upstream to drain, drain to downstream
    P1 = 0.5 * (h_up + h_up * (1 - drain_pos / B)) * drain_pos
    P2 = 0.5 * (h_up * (1 - drain_pos / B) + h_dw) * (B - drain_pos)

    uplift = P1 + P2
    x1 = drain_pos / 2
    x2 = drain_pos + (B - drain_pos) / 2
    moment = P1 * x1 + P2 * x2
    
    return uplift, moment

# 💻 Interactive dam analysis
def dam_analysis(H, B_bottom, B_top, drain_location):
    # Constants
    gamma_c = 24
    gamma_w = 9.81
    gamma_s = 13
    phi = 35
    cohesion = 0
    wave_pressure = 5
    ice_pressure = 10
    freeboard = 2
    stress_allow = 3000
    H_dw = H / 3

    # Geometry & weight
    A_dam = H * (B_bottom + B_top) / 2
    W_dam = gamma_c * A_dam
    x_W = (B_bottom**2 + 2*B_bottom*B_top + B_top**2) / (3*(B_bottom + B_top))

    # Hydrostatic & external pressures
    H_eff = H - freeboard
    P_upstream = 0.5 * gamma_w * H_eff**2
    x_upstream = H_eff / 3

    P_sediment = 0.5 * gamma_s * H_eff**2
    x_sed = H_eff / 3

    P_tail = 0.5 * gamma_w * H_dw**2
    x_tail = H_dw / 3

    P_wave = wave_pressure * H_eff
    x_wave = H_eff / 2

    P_ice = ice_pressure * H_eff
    x_ice = H_eff / 2

    # 💧 Uplift pressure adjusted by drain
    uplift_force, M_uplift = adjusted_uplift(B_bottom, H_eff, H_dw, gamma_w, drain_location)

    # 🔁 Vertical resisting force
    R_vert = W_dam - uplift_force
    resist_force = R_vert * np.tan(np.radians(phi)) + cohesion * B_bottom

    # 🔁 Horizontal load & moments
    P_horz = P_upstream + P_sediment + P_wave + P_ice - P_tail
    M_resist = W_dam * x_W
    M_overturn = (
        P_upstream * x_upstream + P_sediment * x_sed +
        P_wave * x_wave + P_ice * x_ice - P_tail * x_tail
    )

    FS_sliding = resist_force / P_horz
    FS_overturn = (M_resist - M_uplift) / M_overturn
    stress_avg = R_vert / B_bottom
    stress_max = 2 * R_vert / B_bottom

    # 🧱 Dam geometry plot
    x_left = (B_bottom - B_top) / 2
    x_right = x_left + B_top
    dam_x = [0, x_left, x_right, B_bottom, 0]
    dam_y = [0, H, H, 0, 0]

    plt.figure(figsize=(14, 5))

    # Dam profile
    plt.subplot(1, 3, 1)
    plt.plot(dam_x, dam_y, color='black', linewidth=2)
    plt.fill(dam_x, dam_y, color='lightgray')
    plt.axvline(x=drain_location, color='blue', linestyle='--', label='Drain Location')
    plt.title("Dam Geometry with Drain")
    plt.xlabel("Width (m)")
    plt.ylabel("Height (m)")
    plt.legend()
    plt.grid(True)

    # Forces bar chart
    plt.subplot(1, 3, 2)
    labels = ['Weight', 'Uplift', 'Water', 'Sediment', 'Wave', 'Ice', 'Tailwater']
    forces = [W_dam, -uplift_force, P_upstream, P_sediment, P_wave, P_ice, -P_tail]
    colors = ['gray', 'lightblue', 'blue', 'brown', 'skyblue', 'purple', 'navy']
    plt.bar(labels, forces, color=colors)
    plt.xticks(rotation=45)
    plt.title("External Forces (kN/m)")
    plt.ylabel("Force")

    # Moments pie chart
    plt.subplot(1, 3, 3)
    moment_labels = ['Water', 'Sediment', 'Wave', 'Ice']
    moments = [P_upstream * x_upstream, P_sediment * x_sed,
               P_wave * x_wave, P_ice * x_ice]
    plt.pie(moments, labels=moment_labels, autopct='%1.1f%%', startangle=90,
            colors=['blue', 'brown', 'skyblue', 'purple'])
    plt.title("Overturning Moment Contributions")

    plt.tight_layout()
    plt.show()

    # 📋 Stability summary
    print("📋 Dam Stability Summary")
    print(f"Self-Weight: {W_dam:.2f} kN/m")
    print(f"Uplift Force (adjusted): {uplift_force:.2f} kN/m")
    print(f"Total Horizontal Load: {P_horz:.2f} kN/m")
    print(f"FS (Sliding): {FS_sliding:.2f}")
    print(f"FS (Overturning): {FS_overturn:.2f}")
    print(f"Max Toe Stress: {stress_max:.2f} kN/m² → {'Safe' if stress_max <= stress_allow else 'Overstressed'}")

# 🎛️ Interactive sliders
H_slider = widgets.FloatSlider(value=30, min=10, max=50, step=1, description='Dam Height (m)')
B_bottom_slider = widgets.FloatSlider(value=20, min=10, max=40, step=1, description='Bottom Width (m)')
B_top_slider = widgets.FloatSlider(value=6, min=2, max=20, step=1, description='Top Width (m)')
drain_slider = widgets.FloatSlider(value=10, min=1, max=39, step=0.5, description='Drain Location (m)')

ui = widgets.VBox([H_slider, B_bottom_slider, B_top_slider, drain_slider])
out = widgets.interactive_output(dam_analysis, {
    'H': H_slider,
    'B_bottom': B_bottom_slider,
    'B_top': B_top_slider,
    'drain_location': drain_slider
})

display(ui, out)

Dam Stability Analysis Report#

This report summarizes the stability analysis of a gravity dam using hydrostatic, sediment, wave, and ice pressures. Uplift pressure is adjusted based on the location of a drainage gallery. The dam is evaluated for sliding, overturning, and toe stress safety.

🧱 Geometry & Inputs#

Parameter

Value

Units

Dam Height ( H )

30.0

m

Bottom Width ( B_{\text{bottom}} )

20.0

m

Top Width ( B_{\text{top}} )

6.0

m

Drain Location from Upstream

10.0

m

Concrete Unit Weight ( \gamma_c )

24.0

kN/m³

Water Unit Weight ( \gamma_w )

9.81

kN/m³

Sediment Unit Weight ( \gamma_s )

13.0

kN/m³

Soil Friction Angle ( \phi )

35.0

degrees

Cohesion

0.0

kPa

Wave Pressure

5.0

kN/m²

Ice Pressure

10.0

kN/m²

Freeboard

2.0

m

Allowable Toe Stress

3000.0

kN/m²

Uplift Pressure Adjustment#

  • Effective Head: \(( H_{\text{eff}} = H - \text{Freeboard} = 28.0 \, \text{m} \))

  • Tailwater Depth: \(( H_{\text{dw}} = H / 3 = 10.0 \, \text{m} \))

  • Drain Location: 10.0 m from upstream face

  • Adjusted Uplift Force: 1374.0 kN/m

  • Uplift Moment: 13740.0 kN·m

External Forces#

Force Type

Magnitude (kN/m)

Self-Weight

14400.0

Uplift (adjusted)

-1374.0

Upstream Water

3840.0

Sediment

5100.0

Wave

140.0

Ice

280.0

Tailwater

-480.0

Moment Analysis#

Moment Source

Contribution (kN·m)

Upstream Water

1280.0

Sediment

1700.0

Wave

1960.0

Ice

3920.0

Tailwater

-160.0

Uplift

-13740.0

Self-Weight

9600.0

Stability Results#

Check

Value

Status

FS (Sliding)

1.42

✅ Safe

FS (Overturning)

0.85

⚠️ Unsafe

Max Toe Stress

1374.0

✅ Below Limit

Visualization Summary#

  • Dam Geometry: Trapezoidal profile with labeled drain location

  • Force Distribution: Bar chart showing magnitude and direction

  • Moment Contributions: Pie chart highlighting overturning sources

  • Interpretation: Uplift and overturning dominate instability; heel extension or drainage optimization recommended

References#

  • USBR Design Standards for Gravity Dams

  • FHWA Hydraulic Engineering Circulars

  • Bowles, J.E. (1996). Foundation Analysis and Design

  • IS 6512: Criteria for Design of Gravity Dams

💡 Consider increasing heel width, optimizing drain location, or adding shear keys to improve sliding and overturning resistance.

3. Self-Assessment#

Interactive Gravity Dam Stability Analysis — Full Documentation#

This Markdown document provides a complete overview of the interactive trapezoidal gravity dam model, including conceptual understanding, reflection prompts, governing equations, and an engineering quiz to reinforce learning. The model evaluates dam stability under various load conditions and allows users to explore how geometry and drainage location affect performance.

Conceptual Overview#

A gravity dam relies on its mass to resist horizontal forces from water, sediment, and environmental loads. This tool models a trapezoidal dam cross-section and calculates:

  • Structural weight and moment resistance

  • Hydrostatic, wave, and ice pressures

  • Sediment and tailwater loads

  • Uplift pressure adjusted by user-defined drain location

Safety factors against sliding, overturning, and toe stress are evaluated using engineering equilibrium principles.#

###Reflective Questions

  • 💭 How does changing the base width influence dam safety?

  • 💭 Why is the location of drainage galleries important for managing uplift?

  • 💭 What environmental factors contribute to non-hydrostatic forces on a dam?

  • 💭 How do tailwater conditions help resist overturning?

  • 💭 What trade-offs exist between material cost and dam safety?

Governing Equations#

Geometry and Weight#

  • Area: \(( A_{\text{dam}} = H \cdot \frac{B_{\text{bottom}} + B_{\text{top}}}{2} \))

  • Weight: \(( W = \gamma_c \cdot A_{\text{dam}} \))

  • Centroid:
    \(( x_W = \frac{B_{\text{bottom}}^2 + 2B_{\text{bottom}}B_{\text{top}} + B_{\text{top}}^2}{3(B_{\text{bottom}} + B_{\text{top}})} \))

Horizontal Loads#

  • Upstream Pressure:
    \(( P_{\text{upstream}} = \frac{1}{2} \cdot \gamma_w \cdot H_{\text{eff}}^2 \))
    \(( x_{\text{upstream}} = \frac{H_{\text{eff}}}{3} \))

  • Sediment Pressure:
    \(( P_{\text{sediment}} = \frac{1}{2} \cdot \gamma_s \cdot H_{\text{eff}}^2 \))
    \(( x_{\text{sediment}} = \frac{H_{\text{eff}}}{3} \))

  • Wave Load:
    \(( P_{\text{wave}} = P_w \cdot H_{\text{eff}} \))
    \(( x_{\text{wave}} = \frac{H_{\text{eff}}}{2} \))

  • Ice Load:
    \(( P_{\text{ice}} = P_i \cdot H_{\text{eff}} \))
    \(( x_{\text{ice}} = \frac{H_{\text{eff}}}{2} \))

  • Tailwater Resistance:
    \(( P_{\text{tail}} = \frac{1}{2} \cdot \gamma_w \cdot \left(\frac{H}{3}\right)^2 \))
    \(( x_{\text{tail}} = \frac{H/3}{3} \))

Uplift Force (Drain-Adjusted)#

Let ( d ) be drain location from upstream toe and ( B ) the base width:

  • Zone 1:
    \(( P_1 = \frac{1}{2} \cdot \left(h_{\text{up}} + h_{\text{up}} \cdot \left(1 - \frac{d}{B}\right)\right) \cdot d \))
    \(( x_1 = \frac{d}{2} \))

  • Zone 2:
    \(( P_2 = \frac{1}{2} \cdot \left(h_{\text{up}} \cdot \left(1 - \frac{d}{B}\right) + h_{\text{dw}}\right) \cdot (B - d) \))
    \(( x_2 = d + \frac{B - d}{2} \))

  • Uplift Force: \(( P_{\text{uplift}} = P_1 + P_2 \))

  • Uplift Moment: \(( M_{\text{uplift}} = P_1 \cdot x_1 + P_2 \cdot x_2 \))

Stability Analysis#

  • Sliding Safety Factor:
    \(( FS_{\text{sliding}} = \frac{R_{\text{vert}} \cdot \tan(\phi) + c \cdot B}{P_{\text{horizontal}}} \))

  • Overturning Safety Factor:
    \(( FS_{\text{overturning}} = \frac{M_{\text{resist}} - M_{\text{uplift}}}{M_{\text{overturning}}} \))

  • Toe Stress:
    \(( \text{Stress}_{\text{max}} = \frac{2 \cdot R_{\text{vert}}}{B} \))

✅ Quiz#

2. Which equation calculates hydrostatic pressure on the dam’s upstream face?#

  • \(( P_{\text{upstream}} = \frac{1}{2} \cdot \gamma_w \cdot H^2 \))

  • \(( P = \gamma_w \cdot H \))

  • \(( P = \gamma_c \cdot A_{\text{dam}} \))

  • \(( P = \frac{1}{2} \cdot \gamma_s \cdot H^2 \))

3. What is the formula for sliding factor of safety?#

  • \(( FS = \frac{R_{\text{vert}} \cdot \tan(\phi) + c \cdot B}{P_{\text{horizontal}}} \))

  • \(( FS = \frac{M_{\text{resist}}}{M_{\text{overturn}}} \))

  • \(( FS = \frac{P_{\text{upstream}}}{P_{\text{tail}}} \))

  • \(( FS = \frac{R_{\text{vert}}}{B} \))

4. How does increasing base width affect dam stability?#

  • Decreases sliding FS

  • Increases overturning FS

  • Increases uplift pressure

  • Decreases dam’s weight

5. Why is the centroid location important?#

  • Determines maximum stress

  • Used to calculate resisting moment

  • Indicates uplift peak

  • Determines dam height

This interactive model links geometry, physics, and design intuition into a full dam engineering dashboard. Adjust, reflect, and learn from every angle 💧📐🧱.

Contents